2017-06-15: Autonomy Incubator Intern Javier Puig-Navarro Expands Collision Avoidance Algorithm

Javier explains non-Euclidian geometry to me, someone who had to take
Appreciation of Math in college because I didn't make the cut for calculus.

UIUC PhD candidate Javier Puig-Navarro is the professor of the Autonomy Incubator's summer intern squad. Over the four years he's returned to the Ai, he's become the go-to person for everything from math to physics to MatLab questions because he's such a clear, patient teacher. Today, when Javier called me over on my way to the coffee pot, I knew I was about to do some serious learning.

"So, you remember my GJK algorithm that I started working on last summer, right?" he said.

"Yeah, Minkowski Additions and stuff," I replied, eloquently.

Javier's work at the Ai concentrates on collision detection and avoidance, using polytopes and a tricky bit of math called the Minkowski Addition to determine if two UAVs will collide. If the polytopes representing the two vehicles intersect, then that means they're on a collision course. It's completely explained in the blog post from last summer, which I'll link again here.

Javier's algorithm will also move one of the shapes so that they no longer overlap, thereby avoiding the collision. When it does this, he wants to make sure his algorithm chooses which direction to correct a collision in a truly random way— not favoring displacing the polytope upwards over displacing it sideways, for example. It's called removing algorithm bias, and Javier assures me it's very hot right now.

As he works on correcting his algorithm bias, Javier needed a way to visualize distance and direction, to make sure his algorithm is choosing completely randomly. To do that, he built a program that creates 2D and 3D balls of a given circumference— what he called me over to take a look at. There's about to be a lot of math happening, but it's cool math! Ready?

This sphere and circle are generally what we think of when we hear the word "ball." They're defined by Euclidean distance— each of the points on the circumference is the same distance away from the center point if you use this formula:

Euclidean norm 

 This is the geometry you learned in ninth grade. However, it is by no means the only definition of a mathematical "ball." Look at this other visualization from Javier's algorithm.

This diamond thing is also a ball, according to math, because all of the points are equidistant from the center when you calculate them this way instead of the Euclidean way: 

Sum norm

As you can see, this is called the sum norm, or norm 1. The Euclidean Norm, predictably, is called norm 2. So, norm 1 is a diamond and norm 2 is a sphere. There is also an infinity norm, and it looks like this:

 A cube! That's also a ball in this case, if you calculate the distance from the center like this:

Infinity norm

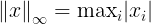
That's the three main norms: 1, 2, and infinity. However, there are infinite norms between those norms. Like, what would norm 3 look like?

A cube with rounded edges, because it's on the spectrum between a sphere (2) and a cube (infinity). So really, distance can be visualized in infinite ways, on a sliding scale from diamond to sphere to cube. Isn't that the wildest?

"So, you need all of these to get rid of your algorithm bias?" I asked.

"No, I actually only need the 2 norm," Javier said. "I just thought this was a good conceptualization for you."

The Autonomy Incubator and Javier Puig-Navarro: bringing you a college-level math lesson to go with your regularly scheduled UAV content. Thanks, Javier!